Sangaku, geometrijska slagalica
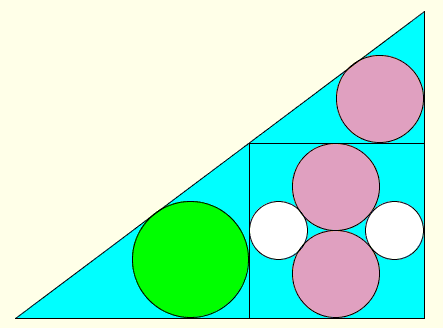
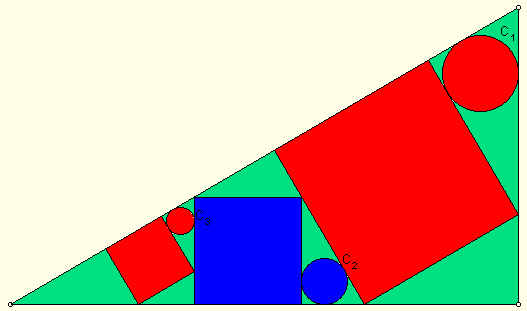
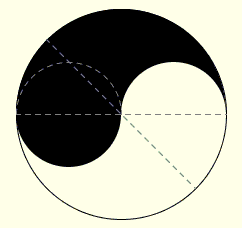
Dva roze kruga radijusa r, i dva bela kruga radijusa t upisani su u kvadrat kao sto je pokazano. Kvadrat sam, je upisan u veliki trougao, i kao sto je ilustrovano, dva kruga radijusa R i r, su upisani u male trouglove izvan kvadrata. Pokazati da je R = 2t.
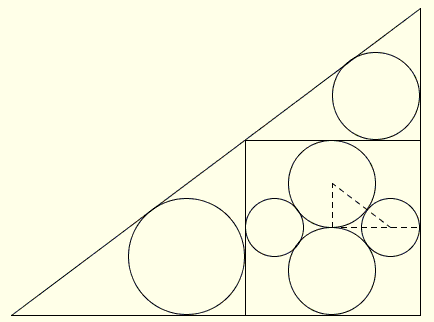
Ocigledno, strana kvadrata je 4r. Primenom Pitagorine teoreme ( u ucrtanom tackastom trouglu), pokazuje da je r = 3t/2. Primenimo ponovo pitagorinu teoremu u malom gornjem trouglu. Moze nas iznenaditi da ispada da je trougao cuveni 3-4-5 ili egipatski trougao sa kracom stranom jednakom 3r. Iz slicnosti ova tri trougla izlazi da svaki ima proporcije 3-4-5 sto navodi da je 4r = 3R. I konacno, R = 4r/3 = 2t
Reference:
# H. Fukagawa, A. Rothman, Drevna Mathematika: Geometrija japanskih hramova, Princeton University Press
http://www.princeton.edu/main/news/archive/S15/04/04O77/index.xml
[Ovu poruku je menjao boxxter dana 25.07.2010. u 20:37 GMT+1]
Dakle, ako je neko dosad i sumnjao da li ti samo prenosiš razne stvari koje iskopaš po Internetu — praveći se da znaš o čemu govoriš, a u stvari ne razumevajući ni najosnovnije pojmove — upravo si izuzetno efektno dokazao da je zaista tako. Ti teoremu koja se na engleskom zove Carpets Theorem, u prevodu teorema o tepisima, ovde nazivaš „Carpet-ova teorema“. Urnebesno. 
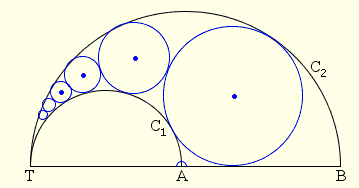
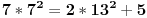
Re: Sangaku, geometrijska slagalica
.
