elitemadzone.org - Koren iz negativnog broja?

dusanboss

Član broj: 329401
Poruke: 856
*.dynamic.isp.telekom.rs.

Jabber: dusanboss

+610 Profil

^{30.11.2017. u 00:39 - pre 87 meseci}

Auu bre . A ja mislio da je meni dosadno i da ne znam šta ću sa sobom.

Dodjem na MadZone i odma se utešim

Bojan Basic
Novi Sad

SuperModerator
Član broj: 6578
Poruke: 3996
*.uns.ac.rs.

Jabber: bojan_basic@elitesecurity.org
ICQ: 305820253

+613 Profil

Re: Koren iz negativnog broja?

^{30.11.2017. u 13:26 - pre 87 meseci}

Citat:

Everick:
Kvadratni koren iz -1 je i.

Nije tačno.

Ljubičice crvena, što si plava kô zelena trava.

Odgovor na temu

stopnarkomaniji

Član broj: 336064
Poruke: 11

+54 Profil

Re: Koren iz negativnog broja?

^{30.11.2017. u 15:18 - pre 87 meseci}

Drži se ti gorile i lava.

Kvadratni koren: http://www.wolframalpha.com/input/?i=sqrt[-1]
==> {+i,-i}

Treći koren: http://www.wolframalpha.com/input/?i=%28-1%29^%281%2F3%29
==> {-1,e^(iπ/3),e^(-iπ/3)}

Četvrti koren: http://www.wolframalpha.com/input/?i=%28-1%29^%281%2F4%29
==> {e^(iπ/4),e^(-iπ/4),e^(3iπ/4),e^(-3iπ/4)}

Odgovor na temu

Java Beograd
Novi Beograd

Član broj: 11890
Poruke: 9840
*.dynamic.isp.telekom.rs.

+10387 Profil

Re: Koren iz negativnog broja?

^{30.11.2017. u 17:03 - pre 87 meseci}

http://lmgtfy.com/?q=square+root+of+-1
http://lmgtfy.com/?q=cube+root+of+-1
http://lmgtfy.com/?q=fourth+root+of+-1

OTPOR blokadi ulica, OTPOR blokiranom Beogradu, OTPOR blokiranoj Srbiji

Odgovor na temu

mjanjic
Šikagou

Član broj: 187539
Poruke: 2951

+757 Profil

Re: Koren iz negativnog broja?

^{30.11.2017. u 22:35 - pre 87 meseci}

Postoji u matematici dva slučaja koja su suštinski različita:

Dakle, ako se gleda rešenje kvadratne jednačine, onda ih ima dva, a ako se gleda samo vrednost korena, onda ima jedna.
Ove dve jednakosti (pod 1. i 2. sa leve strane) nisu identične, tj. prva je kvadratna jednačina, a druga je samo vrednost koja se dodeljuje promenljivoj x.
Za drugi izraz se ne može reći da je koren iz -1 jednako -i samo zato što jednakost važi nakon kvadriranja obe strane (čime se dobija jednakost 1.), jer se kvadriranjem upravo gubi informacija o predznaku.
Zato je koren iz 4 uvek jednako 2, a nikada -2, iako je kvadrat oba broja jednak 4, a -2 se dobija jedino kao

.

Zato se nakon eventualnog kvadriranja obe strane jednakosti pri rešavanju jednačina ili proveravanju jednakosti obavezno vodi računa o tome da se nakon proveri koja rešenja zadovoljavaju polaznu jednakost.

Blessed are those who can laugh at themselves, for they shall never cease to be amused.

Odgovor na temu

djoka_l
Beograd

Član broj: 56075
Poruke: 3547

Jabber: djoka_l

+1510 Profil

Re: Koren iz negativnog broja?

^{01.12.2017. u 08:50 - pre 87 meseci}

Citat:

mjanjic:
Postoji u matematici dva slučaja koja su suštinski različita:

Kvadratna jednačina je specijalan slučaj, možemo da posmatramo i opštije:

Ako predstavimo kompleksni broj u trigonometrijskom obliku ili eksponencijalnom imamo da je

zbog periodičnosti
tada su rešenja (ako postoje) oblika

U slučaju

pa je

jednačina ima beskonačno mnogo rešenja, ali samo dva različita: 1 i -1

Odgovor na temu

Bojan Basic
Novi Sad

SuperModerator
Član broj: 6578
Poruke: 3996
87.116.176.*

Jabber: bojan_basic@elitesecurity.org
ICQ: 305820253

+613 Profil

Re: Koren iz negativnog broja?

^{01.12.2017. u 15:19 - pre 87 meseci}

Citat:

mjanjic:

Dakle, ako se gleda rešenje kvadratne jednačine, onda ih ima dva, a ako se gleda samo vrednost korena, onda ima jedna.

Baš u tome je problem: koju jednu vrednost ćeš izabrati za

, hoće li to biti

ili

? Ako je koren realan, onda postoji konvencija po kojoj za koren uzimamo nenegativnu vrednost, pa stoga kažemo

a ne

. Međutim, ako je koren kompleksan, kako u skupu kompleksnih brojeva nemamo podelu na pozitivne i negativne (niti neko adekvatno uopštenje), stoga kompleksan koren možemo posmatrati jedino kao višeznačnu funkciju. Dakle, ako hoćete bilo šta da kažete za

, još bi i moglo

, ali nikako

Ljubičice crvena, što si plava kô zelena trava.

Odgovor na temu

stopnarkomaniji

Član broj: 336064
Poruke: 11

+54 Profil

Re: Koren iz negativnog broja?

^{01.12.2017. u 16:22 - pre 87 meseci}

U udžbeniku iz matematike za srednju školu
jasno stoji

Citat:

definišimo i = √-1

Dakle, učenik se sreće sa definicijom a ne izvodjenjem.
Zato neće ni razmišljati o mogućnosti da postoji više vrednosti.

Otuda stalno konfliktne diskusije o vrednosti korena negativnog broja.

Odgovor na temu

Everick

Član broj: 337519
Poruke: -1
*.dynamic.isp.telekom.rs.

+15 Profil

Re: Koren iz negativnog broja?

^{01.12.2017. u 21:41 - pre 87 meseci}

Mislim da je vreme da se Nedeljko ovde umeša. Ipak je Nedeljko neprevaziđen po pitanju matematike ovde na forumu.

Odgovor na temu

mjanjic
Šikagou

Član broj: 187539
Poruke: 2951

+757 Profil

Re: Koren iz negativnog broja?

^{01.12.2017. u 23:01 - pre 87 meseci}

Ako ćemo "mak na konac", pogledajte lepo definiciju za polje kompleksnih brojeva, kao i kako se definiše imaginarna jedinica. Evo, na primer ovde: http://imft.ftn.uns.ac.rs/~vanja/old/P4.pdf

Nigde se tu ne pominje koren iz minus jedan, već skup uređenih parova realnih brojeva (a,b) sa operacijama na tom skupu (sabiranje i množenje kao binarne, kao i dve unarne operacije).

Tu se lepo za par (0,1) kaže da predstavlja imaginarnu jedinicu, kao i da je (0,1)·(0,1) = -1.
I gde se tu pominje koren iz minus jedan?

Ono što jeste prihvatljivo je u stvari

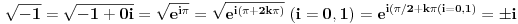
, odakle sledi da koren iz -1 ima dve vrednosti, međutim ovde se koren iz -1 posmatra kao koren kompleksnog, a ne koren realnog broja, pa zato ima dva rešenja. Zato se na višem nivou i ne govori o korenu iz -1 kao imaginarnoj jedinici, jer se radi o krenu kompleksnog broja koji ima dve vrednosti, ali se jednakost

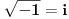
uvodi u srednjoj školi kao analogna korenu pozitivnog realnog broja, a i da bi učenici kasnije manje imali problema sa shvatanjem konjugovano-kompleksnih brojeva i sl.
Inače, parovi konjugovano-kompleksnih brojeva su uvek rešenja kubne jednačine sa realnim koeficijentima kada je samo jedno rešenje realno, a i kvadratnih jednačina sa realnim koeficijentima koje nemaju realna rešenja (što je očigledno iz opšte formule za rešenja kada je diskriminanta negativna).

Blessed are those who can laugh at themselves, for they shall never cease to be amused.

Odgovor na temu

Everick

Član broj: 337519
Poruke: -1
*.dynamic.isp.telekom.rs.

+15 Profil

Re: Koren iz negativnog broja?

^{03.12.2017. u 14:44 - pre 87 meseci}

Koliki je kvadratni koren iz -i?

Odgovor na temu

Java Beograd
Novi Beograd

Član broj: 11890
Poruke: 9840
*.dynamic.isp.telekom.rs.

+10387 Profil

Re: Koren iz negativnog broja?

^{03.12.2017. u 14:52 - pre 87 meseci}

http://lmgtfy.com/?q=square+root+of+-i

OTPOR blokadi ulica, OTPOR blokiranom Beogradu, OTPOR blokiranoj Srbiji

Odgovor na temu

Bradzorf012
Mile i ortaci LLC

Član broj: 334105
Poruke: 466

+1020 Profil

Re: Koren iz negativnog broja?

^{03.12.2017. u 15:40 - pre 87 meseci}

mjanjic

Najpre si lepo objasnio u prvom javljanju, a onda si u drugom rekao da koren ima dve vrednosti. Ne može da ima dve vrednosti, jer to onda nije funkcija. Što kaže Bojan, "višeznačna funkcija", ali to onda nije funkcija. Ok, može biti da ima više vrednosti u jednoj tački, ali su onda u pitanju različite grane iste funkcije, što ovde nije slučaj. Dakle

jednačina x² = a za a >= 0 ima dva rešenja: -1 i 1, tj. √a i -√a.

Šta uzeti kao √a za a < 0 je već drugo pitanje.

Odgovor na temu

Braxi

Član broj: 333132
Poruke: 335

+384 Profil

Re: Koren iz negativnog broja?

^{04.12.2017. u 10:14 - pre 87 meseci}

jaoj kad se setim kompleksne analize. Nikad vise !

Odgovor na temu

stopnarkomaniji

Član broj: 336064
Poruke: 11

+54 Profil

Re: Koren iz negativnog broja?

^{04.12.2017. u 23:14 - pre 87 meseci}

Komrad Bradzorf

Zar se ne kaže "u jednoj tačci"?

To ne znam zašto se tako kaže.
Ali kad je reč o višeznačnim funkcijama onda
preslikavanje F:M --> P(C) se naziva višeznačna funkcija.

Ako je f: M --> C neprekidno preslikavanje i f(z) element F(z) za z element M
tada je f grana višeznačne funkcije F.

U tom smislu, koren je višeznačna funkcija.
Jer w = z^(1/n), n element N\{1} i koren se definiše kao rešenje jednačine
w^n = z
stoga je F(z) = z^(1/n) višeznačna funkcija.

Odgovor na temu

Java Beograd
Novi Beograd

Član broj: 11890
Poruke: 9840
93.186.70.*

+10387 Profil

Re: Koren iz negativnog broja?

^{05.12.2017. u 06:45 - pre 87 meseci}

Citat:

stopnarkomaniji: Zar se ne kaže "u jednoj tačci"?

Ako može "vrednosti u tačci", onda može i "džigerica mačci". Ali, kao što znamo, džigerica se daje mački, a ne mačci.

OTPOR blokadi ulica, OTPOR blokiranom Beogradu, OTPOR blokiranoj Srbiji

Odgovor na temu